引き続きPyTorch Tutorialを見て行きます。今回は、NEURAL NETWORKSです。（以下翻訳です）

Neural Network

NNはtorch.nn packageを使って構築します。

前回autogradの勉強をしましたので、modelを定義し勾配計算を行う際にnnがautogradに依存していることは理解されていると思います。nn.Moduleはlayerを構成し、forward(input) methodは出力を返します。

下の手書き文字認識のnetworkを見てみましょう: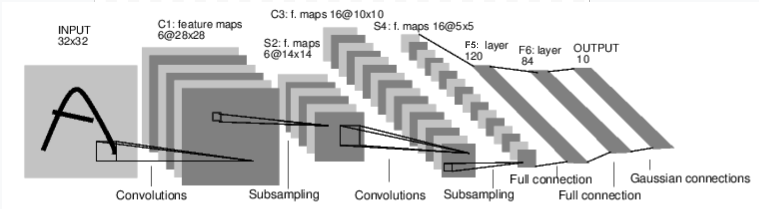

convnet

簡単なfeed-forward networkです。入力があり、それをいくつかのlayerにつぎつぎに手渡していき、最後に出力を得ます。

NNにおける典型的な学習過程は以下の通りです:

• 学習可能な変数（あるいは重み）をもつNNを定義する
• データセットを繰り返し入力する
• 入力をnetworkで処理する
• lossを計算する（出力が正解からどれだけ離れているか）
• Networkの変数に勾配を逆伝搬して行きます
• Networkの重みを更新します。通常は簡単な更新規則で行われます: weight = weight – learning rate * gradient

Networkの定義

以下のようなnetworkを定義します:

import torch
import torch.nn as nn
import torch.nn.functional as F

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        # 1 input image channel, 6 output channels, 3x3 square convolution
        # kernel
        self.conv1 = nn.Conv2d(1, 6, 3)
        self.conv2 = nn.Conv2d(6, 16, 3)
        # an affine operation: y = Wx + b
        self.fc1 = nn.Linear(16 * 6 * 6, 120)  # 6*6 from image dimension
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)
    def forward(self, x):
        # Max pooling over a (2, 2) window
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
        # If the size is a square you can only specify a single number
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)
        x = x.view(-1, self.num_flat_features(x))
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x
    def num_flat_features(self, x):
        size = x.size()[1:]  # all dimensions except the batch dimension
        num_features = 1
        for s in size:
            num_features *= s
        return num_features

net = Net()
print(net)

Out:

Net(
  (conv1): Conv2d(1, 6, kernel_size=(3, 3), stride=(1, 1))
  (conv2): Conv2d(6, 16, kernel_size=(3, 3), stride=(1, 1))
  (fc1): Linear(in_features=576, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)

forward関数を定義すれば、勾配計算を行うbackward関数はautogradで自動的に定義されます。forward関数ではすべてのtensor演算を使用できます。

Model内の学習可能な変数はnet.parameters()で確認できます。

params = list(net.parameters())
print(len(params))
print(params[0].size())  # conv1's .weight

Out:

10
torch.Size([6, 1, 3, 3])

32×32のrandomな入力を試してみましょう。このnetwork (LeNet)は32×32の入力サイズを仮定しているので、このnetworkでMNIST datasetを使う際は個々のdataのsizeを32×32にresizeしてください。

input = torch.randn(1, 1, 32, 32)
out = net(input)
print(out)

Out:

tensor([[ 0.1464,  0.0673, -0.0185,  0.0048,  0.1427, -0.0866, -0.0237, -0.0991,
         -0.0903,  0.0886]], grad_fn=<AddmmBackward>)

すべての変数の勾配値をzeroで初期化し、randomな勾配値で逆伝搬させます:

net.zero_grad()
out.backward(torch.randn(1, 10))

Note: torch.nnはmini-batchのみ利用可能、すなわちtorch.nn packageではおしなべてsample dataのmini-batchのみを入力として扱います。単一のsample dataは入力として受け付けません。

たとえば、nn.Conv2dはn Sample x m Channel x Height x Widthの4次元tensorを取り込みます。

単一sample dataを喰わせたい場合は、input.unsqueeze(0)を使うことによりbatchの次元をだまし、扱うことができます。

先に進む前に、ここまでの要点を振り返っておきましょう:

• torch.Tensor – backward()のようなautograd演算がsupportされた複数次元arrayのこと。Tensorの勾配も保持する。
• nn.Module – Neural network moduleのこと。GPUへのmoveやexport, loadなど変数を扱う上で便利な機能を持つ。
• nn.Parameter – Tensorのようなもの。Moduleに属性が指定された際に変数として自動的に登録される。
• autograd.Function – autograd演算のforwardやbackward機能の実装がある。すべてのtensor演算は少なくともひとつのFunctionを持ち、tensorやその履歴を生成保持する機能を持つ。

以下の説明が終わりました:

• NNの定義
• 入力を処理し、backwardを呼ぶ

これから以下の説明をはじめます:

• lossの計算
• Networkの重みの更新

Loss関数

Loss関数は(output, target)のpairを入力として持ち、出力が目標値からどれだけ離れているかを推定し、その距離を数値として計算します。

nn packageにはいくつかのloss関数があります。簡単なlossとしてはnn.MSELossがあり、出力と目標値の二乗平均誤差を用います。

例:

output = net(input)
target = torch.randn(10)  # a dummy target, for example
target = target.view(1, -1)  # make it the same shape as output
criterion = nn.MSELoss()

loss = criterion(output, target)
print(loss)

Out:

tensor(1.0942, grad_fn=<MseLossBackward>)

逆伝搬の中でlossを追跡したい場合は、.grad_fn属性を見ることにより、以下のような計算graphを得ます:

input -> conv2d -> relu -> maxpool2d -> conv2d -> relu -> maxpool2d
      -> view -> linear -> relu -> linear -> relu -> linear
      -> MSELoss
      -> loss

loss.backward()が呼ばれるとすべてのgraphのlossが微分され、requires_grad=Trueが指定されたすべてのtensorの.grad tensorに勾配値が蓄積されます。

逆伝搬stepを少し可視化してみましょう:

print(loss.grad_fn)  # MSELoss
print(loss.grad_fn.next_functions[0][0])  # Linear
print(loss.grad_fn.next_functions[0][0].next_functions[0][0])  # ReLU

Out:

<MseLossBackward object at 0x7fe290dfb390>
<AddmmBackward object at 0x7fe290dfb978>
<AccumulateGrad object at 0x7fe290dfb978>

逆伝搬

loss.backward()を呼ぶと、誤差が逆伝搬します。今ある勾配情報をclearしなければ、今ある情報に新しい勾配値が追記されます。

ここで、loss.backward()を呼んだときのconv1のbias勾配の変化を見てみましょう。

net.zero_grad()     # zeroes the gradient buffers of all parameters

print('conv1.bias.grad before backward')
print(net.conv1.bias.grad)

loss.backward()

print('conv1.bias.grad after backward')
print(net.conv1.bias.grad)

Out:

conv1.bias.grad before backward
tensor([0., 0., 0., 0., 0., 0.])
conv1.bias.grad after backward
tensor([-0.0068, -0.0244,  0.0278, -0.0142,  0.0111, -0.0078])

以上がloss関数の動作でした。

追加情報: 深層NNを構築するために、NN packageにはさまざまな種類のmoduleやloss関数が用意されています。一覧と説明はこちらを参照ください。

残るはこちらです:

• Networkの重みの更新

重みの更新

最も簡単で実用的な更新規則は、確率的勾配降下法（Stochastic Gradient Descent (SGD)）です: weight = weight – learning_rate * gradient

簡単なPython codeでこれを実現できます:

learning_rate = 0.01
for f in net.parameters():
    f.data.sub_(f.grad.data * learning_rate)

しかしながら、NNを扱う場合、SGD以外にもNesterov-SGD, Adam, RMSPropなどさまざまな更新規則を使いたいと思います。torch.optimという小さなpackage にこれらすべての実装が用意されています。使い方は簡単です:

import torch.optim as optim

# create your optimizer
optimizer = optim.SGD(net.parameters(), lr=0.01)

# in your training loop:
optimizer.zero_grad()   # zero the gradient buffers
output = net(input)
loss = criterion(output, target)
loss.backward()
optimizer.step()    # Does the update

Note: なぜ勾配bufferを明示的にoptimizer.zero_grad()でzero clearしているのかと言うと、逆伝搬のsectionで説明したとおり、clearしないと過去の勾配値が蓄積されるからです。

全Scriptの計算時間: ( 0 minutes 0.045 seconds)

さいごに

勉強になりましたね ? 結構細かいtipsが散りばめられていたと思います。次回でこのblitzは最後になりますが、引き続きTutorialを見て行きましょう !

関連記事